

TADA 05
¿Qué es la estadística?
Ciencia que estudia la recolección, análisis e interpretación de datos, ya sea para ayudar en la resolución de la toma de decisiones o para explicar condiciones regulares o irregulares de algún fenómeno o estudio aplicado, de ocurrencia en forma aleatoria o condicional.
Videos para comprender más a fondo el término:
https://www.youtube.com/watch?v=Nlfk7kRz2uU
https://www.youtube.com/watch?v=Xq3thcQqwbc
.gif)
Videos para comprender más a fondo el término:
https://www.youtube.com/watch?v=Nlfk7kRz2uU
https://www.youtube.com/watch?v=Xq3thcQqwbc
.gif)
Estadística descriptiva:
Es la rama de la estadística que recolecta, analiza y caracteriza un conjunto de datos (peso de la población, beneficios diarios de una empresa, temperatura mensual,…) con el objetivo de describir las características y comportamientos de este conjunto mediante gráficos.

TODO SOBRE ESTADÍSTICA DESCRIPTIVA:
Estadística inferencial:
Es una parte de la estadística que comprende los métodos y procedimientos para deducir propiedades (hacer inferencias) de una población, a partir de una pequeña parte de la misma (muestra). También permite comparar muestras de diferentes poblaciones.
TODO SOBRE ESTADÍSTICA INFERENCIAL:
VIDEO: Introducción a la estadística
TÉCNICAS DE MUESTREO
- Muestreo aleatorio. Se usa cuando a cada elemento de la población se le quiere dar la misma oportunidad de ser elegido en la muestra.
- Muestreo estratificado. Se usa cuando se conoce de antemano que la población está dividida en estratos, que son equivalentes a categorías y los cuales por lo general no son del mismo tamaño. De cada estrato se toma una muestra aleatoria proporcional al tamaño del estrato.
- Muestreo por conglomerados: La población se divide en grupos llamados conglomerados. Luego se elige al azar un cierto número de ellos y todos los elementos de los conglomerados elegidos forman la muestra.
- Muestreo sistemático. Se usa cuando los datos de la población están ordenados en forma numérica. La primera observación es elegida al azar de entre los primeros elementos de la población y las siguientes observaciones son elegidas guardando la misma distancia entre sí.
-
VIDEO: Técnicas de muestreo
CUARTILES
Los cuartiles son los tres valores que dividen al conjunto de datos ordenados en cuatro partes porcentualmente iguales. El primer cuartil, es el valor en el cual o por debajo del cual queda un cuarto (25%) de todos los valores de la sucesión (ordenada).
Datos agrupados:

k= 1,2,3:
- Lk = Límite real inferior de la clase del cuartil k
- n = Número de datos
- Fk = Frecuencia acumulada de la clase que antecede a la clase del cuartil k.
- fk = Frecuencia de la clase del cuartil k
- c = Longitud del intervalo de la clase del cuartil k
Los deciles son ciertos números que dividen la sucesión de datos ordenados en diez partes porcentualmente iguales. Son los nueve valores que dividen al conjunto de datos ordenados en diez partes iguales..
Datos agrupados:
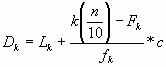
k= 1,2,3,... 9
- Lk = Límite real inferior de la clase del decil k
- n = Número de datos
- Fk = Frecuencia acumulada de la clase que antecede a la clase del decil k.
- fk = Frecuencia de la clase del decil k
- c = Longitud del intervalo de la clase del decil k
Los percentiles son ciertos números que dividen la sucesión de datos ordenados en cien partes porcentualmente iguales. Estos son los 99 valores que dividen en cien partes iguales el conjunto de datos ordenados.
Datos agrupados:

k= 1,2,3,... 99
- Lk = Límite real inferior de la clase del decil k
- n = Número de datos
- Fk = Frecuencia acumulada de la clase que antecede a la clase del decil k.
- fk = Frecuencia de la clase del decil k
- c = Longitud del intervalo de la clase del decil k
TIPOS DE GRÁFICOS
- Gráfico de barras: El más conocido y utilizado de todos los tipos de gráficos es el gráfico o diagrama de barras. En éste, se presentan los datos en forma de barras contenidas en dos ejes cartesianos (coordenada y abscisa) que indican los diferentes valores.
- Gráfico circular: El también muy habitual gráfico en forma de “quesito”, en este caso la representación de los datos se lleva a cabo mediante la división de un círculo en tantas partes como valores de la variable investigada y teniendo cada parte un tamaño proporcional a su frecuencia.

- Histograma: Aunque a simple vista muy semejante al gráfico de barras, el histograma es uno de los tipos de gráfica que a nivel estadístico resulta más importante y fiable. En esta ocasión, también se utilizan barras para indicar a través de ejes cartesianos.
- Gráfico de líneas: En este tipo de gráfico se emplean líneas para delimitar el valor de una variable.. También puede usarse para comparar los valores de una misma variable o de diferentes investigaciones utilizando el mismo gráfico (usando diferentes líneas).
- Gráfico de dispersión: El gráfico de dispersión o gráfico xy es un tipo de gráfico en el cual mediante los ejes cartesianos se representa en forma de puntos todos los datos obtenidos mediante la observación.
MEDIDAS DE TENDENCIA
CENTRAL
Se llama medidas de tendencia central a
los valores numéricos en torno a los cuales se agrupan en mayor o menor medida,
los valores de una variable estadística. Estas medidas se conocen también como
promedios.
Para que un valor pueda ser considerado
promedio, debe cumplirse que esté situado entre el mejor y el mayor de de la
serie y que su cálculo y utilización resulten sencillos en términos
matemáticos.
Media. Un promedio aritmético del
total de datos.
Media para datos no agrupados.
Media para datos agrupados.
Mediana. Se ordenan los datos de
menor a mayor y el que se encuentra justo a la mitad, ese valor corresponde a
la mediana.
Si hay un número par de datos y por ende
no hay un dato en el medio, se toman los dos datos de en medio y se saca un
valor promedio de ambos.
Mediana para datos no agrupados.
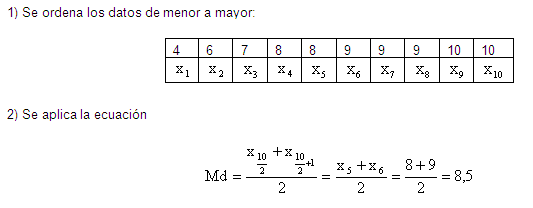
Mediana para datos agrupados.

Moda. Valor que se repite más en nuestros
datos.
Moda para datos agrupados.

MEDIDAS DE DISPERSIÓN
Parámetros estadísticos que indican como
se alejan los datos respecto de la media aritmética. Sirven como indicador de
la variabilidad de los datos. Las medidas de dispersión más utilizadas son el
rango, la desviación estándar y la varianza.
Rango. Intervalo en el que se encuentran
los datos de la muestra.
R= Vmáx. - Vmín.
Desviación media. La desviación respecto
a la media es la diferencia en valor absoluto entre cada valor de la
variable estadística y la media aritmética.

Desviación estándar. La desviación estándar es la medida de dispersión más común, que indica qué
tan dispersos están los datos con respecto a la media. Mientras mayor sea la
desviación estándar, mayor será la dispersión de los datos.
El símbolo σ (sigma) se utiliza
frecuentemente para representar la desviación estándar de una población,
mientras que s se utiliza para representar la desviación estándar de
una muestra.
Desviación estándar para datos no
agrupados.
Desviación estándar para datos agrupados.
Varianza. Es una medida de dispersión
definida como la esperanza del cuadrado de la desviación de dicha variable
respecto a su media.
Varianza para datos no agrupados.

Varianza para datos agrupados.

Enlaces para comprender mejor el tema:
TABLA DE DISTRIBUCIÓN DE FRECUENCIAS
Ejercicio realizado en clase:
Ejercicio realizado en clase:
ALGUNOS EJERCICIOS REALIZADOS EN CLASE, CON AYUDA DEL PROFESOR AGUILAR PÉREZ ENRIQUE. EN UPIICSA
En éstos ejercicios podemos observar la resolución de una serie de problemas, contando con datos agrupados, se realizó una respectiva tabla de distribución frecuencias, para posteriormente calcular la media, mediana, moda, de igual manera, podemos observar la implementación de dos tipos de gráficos (De pastel y de histograma), además de calcular un respectivo cuartil.
A continuación se dejarán vídeos con el fin de mayor aprendizaje:
https://www.youtube.com/watch?v=Eju_9eM4PZg&t=99s



VIDEO: PRUEBAS DE HIPÓTESIS (Pasos)





















TEOREMA DEL LÍMITE CENTRAL
El teorema del límite central o teorema central del límite (el nombre viene de un documento científico escrito por George Pólya en 1920, titulado Über den zentralen Grenzwertsatz der Wahrscheinlichkeitsrechnung und das Momentenproblem [Sobre el «teorema del límite» (Grenzwertsatz) central del cálculo probabilístico y el problema de los momentos] por lo que lo central [importante] es el teorema, no el límite) indica que, en condiciones muy generales, si Sn es la suma de n variables aleatorias independientes y de varianza no nula pero finita, entonces la función de distribución de Sn «se aproxima bien» a una distribución normal (también llamada distribución gaussiana, curva de Gauss o campana de Gauss). Así pues, el teorema asegura que esto ocurre cuando la suma de estas variables aleatorias e independientes es lo suficientemente grande.
VIDEO: Teorema de límite central
Distribución normal
En estadística y probabilidad se llama distribución normal, distribución de Gauss, distribución gaussiana o distribución de Laplace-Gauss, a una de las distribuciones de probabilidad de variable continua que con más frecuencia aparece en estadística y en la teoría de probabilidades.
La gráfica de su función de densidad tiene una forma acampanada y es simétrica respecto de un determinado parámetro estadístico. Esta curva se conoce como campana de Gauss y es el gráfico de una función gaussiana.
La importancia de esta distribución radica en que permite modelar numerosos fenómenos naturales, sociales y psicológicos. Mientras que los mecanismos que subyacen a gran parte de este tipo de fenómenos son desconocidos, por la enorme cantidad de variables incontrolables que en ellos intervienen, el uso del modelo normal puede justificarse asumiendo que cada observación se obtiene como la suma de unas pocas causas independientes.De hecho, la estadística descriptiva sólo permite describir un fenómeno, sin explicación alguna. Para la explicación causal es preciso el diseño experimental, de ahí que al uso de la estadística en psicología y sociología sea conocido como método correlacional.

VIDEO: Distribución normal
Estadística inferencial: Estimación por intervalos de confianza
Dada una variable aleatoria con distribución
Normal N(μ, σ), el objetivo es la construcción de un intervalo de
confianza para el parámetro μ, basado en una muestra de tamaño n de
la variable.
Desde el punto de vista didáctico hemos de
considerar dos posibilidades sobre la desviación típica de la variable: que sea
conocida o que sea desconocida y tengamos que estimarla a partir de la muestra.
El caso de σ conocida, ya comentado anteriormente, no pasa de ser un caso
académico con poca aplicación en la práctica, sin embargo es útil desde del
punto de vista didáctico.
Caso de varianza conocida
Dada una muestra X1,
..., Xn, el estadístico
se distribuye según una Normal estándar. Por tanto,
aplicando el método del pivote podemos construir la expresión
donde zα/2 es el valor
de una distribución Normal estándar que deja a su derecha una probabilidad de α/2, de
la que se deduce el intervalo de confianza
Caso de varianza desconocida
Dada una muestra X1,
..., Xn, el estadístico
se distribuye según una t de
Student de n − 1 grados de libertad. Por tanto, y siguiendo pasos
similares a los del apartado anterior, el intervalo de confianza resultante es
donde tα/2 es el valor
de una distribución t de Student con n − 1 grados de libertad que
deja a su derecha una probabilidad de α/2.
Con el programa siguiente podemos calcular el
intervalo de confianza para la media de una distribución Normal con desviación
típica desconocida.
http://www.ub.edu/stat/GrupsInnovacio/Statmedia/demo/Temas/Capitulo8/B0C8m1t0.htm
VIDEO: Estimación por intervalos de confianza
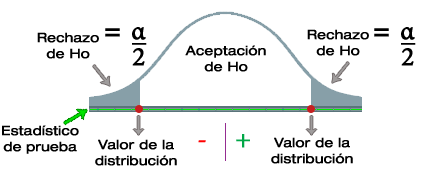
PRUEBAS DE HIPÓTESIS
Una prueba de hipótesis es una regla que especifica si se puede aceptar o rechazar una afirmación acerca de una población dependiendo de la evidencia proporcionada por una muestra de datos.
Una prueba de hipótesis examina dos hipótesis opuestas sobre una población: la hipótesis nula y la hipótesis alternativa. La hipótesis nula es el enunciado que se probará. Por lo general, la hipótesis nula es un enunciado de que "no hay efecto" o "no hay diferencia". La hipótesis alternativa es el enunciado que se desea poder concluir que es verdadero de acuerdo con la evidencia proporcionada por los datos de la muestra.
Con base en los datos de muestra, la prueba determina si se puede rechazar la hipótesis nula. Usted utiliza el valor p para tomar esa decisión. Si el valor p es menor que el nivel de significancia (denotado como α o alfa), entonces puede rechazar la hipótesis nula.
Un error común de percepción es que las pruebas estadísticas de hipótesis están diseñadas para seleccionar la más probable de dos hipótesis. Sin embargo, al diseñar una prueba de hipótesis, establecemos la hipótesis nula como lo que queremos desaprobar. Puesto que establecemos el nivel de significancia para que sea pequeño antes del análisis (por lo general, un valor de 0.05 funciona adecuadamente), cuando rechazamos la hipótesis nula, tenemos prueba estadística de que la alternativa es verdadera. En cambio, si no podemos rechazar la hipótesis nula, no tenemos prueba estadística de que la hipótesis nula sea verdadera. Esto se debe a que no establecimos la probabilidad de aceptar equivocadamente la hipótesis nula para que fuera pequeña.
Entre las preguntas que se pueden contestar con una prueba de hipótesis están las siguientes:
- ¿Tienen las estudiantes de pregrado una estatura media diferente de 66 pulgadas?
- ¿Es la desviación estándar de su estatura igual a o menor que 5 pulgadas?
- ¿Es diferente la estatura de las estudiantes y los estudiantes de pregrado en promedio?
- ¿Es la proporción de los estudiantes de pregrado significativamente más alta que la proporción de las estudiantes de pregrado.

VIDEO: PRUEBAS DE HIPÓTESIS (Pasos)
REGRESIÓN LINEAL

DATOS DISPERSOS, Y LINEA DE AJUSTE, UNA VEZ REALIZADA LA REGRESIÓN LINEAL.
El modelo de pronósstico de regresión lineal permite hallar el valor esperado de una variable aleatoria a cuando b toma un valor específico. La aplicación de este método implica un supuesto de linealidad cuando la demanda presenta un comportamiento creciente o decreciente, por tal razón, se hace indispensable que previo a la selección de este método exista un análisis de regresión que determine la intensidad de las relaciones entre las variables que componen el modelo.

DATOS DISPERSOS, Y LINEA DE AJUSTE, UNA VEZ REALIZADA LA REGRESIÓN LINEAL.
La primera forma de regresión lineal documentada fue el método de los mínimos cuadrados que fue publicada por Legendre en 1805, Gauss publicó un trabajo en donde desarrollaba de manera más profunda el método de los mínimos cuadrados, y en dónde se incluía una versión del teorema de Gauss-Márkov.
El término regresión se utilizó por primera vez en el estudio de variables antropométricas: al comparar la estatura de padres e hijos, donde resultó que los hijos cuyos padres tenían una estatura muy superior al valor medio, tendían a igualarse a éste, mientras que aquellos cuyos padres eran muy bajos tendían a reducir su diferencia respecto a la estatura media; es decir, "regresaban" al promedio. La constatación empírica de esta propiedad se vio reforzada más tarde con la justificación teórica de ese fenómeno.
El término lineal se emplea para distinguirlo del resto de técnicas de regresión, que emplean modelos basados en cualquier clase de función matemática. Los modelos lineales son una explicación simplificada de la realidad, mucho más ágiles y con un soporte teórico mucho más extenso por parte de la matemática y la estadística.
Pero bien, como se ha dicho, se puede usar el término lineal para distinguir modelos basados en cualquier clase de aplicación.
ESTUDIO ESTADÍSTICO: ¿Los alumnos de UPIICSA reprueban por alguna adicción?
Una vez realizadas las 30 encuestas dentro de la UPIICSA se obtuvieron lo siguientes datos:
INFOGRAFÍA: Resultados gráficos del estudio



















INFOGRAFÍA

















